campionamento teorema di Nyquist Shannon
09.04 2020 | by massimilianocampionamento teorema di Nyquist Shannon Per campionamento si intende il “pizzicare” un segnale analogico ogni Tc detto “passo di […]
https://www.ingegnerianetworking.com/wp-content/uploads/2020/04/teorema-nyquist-shannon-a44.png
campionamento teorema di Nyquist Shannon
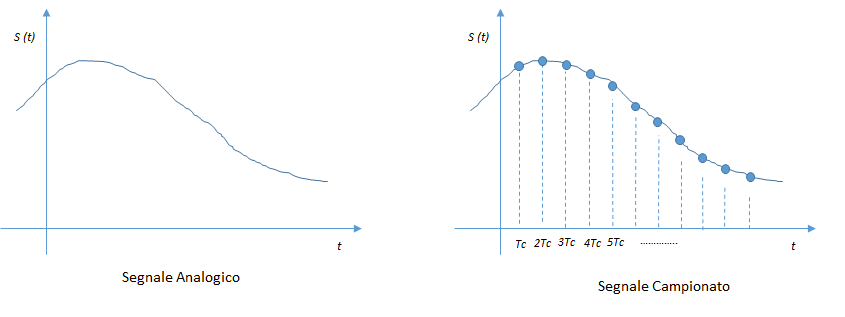
Per campionamento si intende il “pizzicare” un segnale analogico ogni Tc detto “passo di campionamento”
Fc = 1 / Tc è la frequenza di campionamento.
Il teorema di Nyquist-Shannon afferma che se:
s(t) è un segnale a banda limitata ovvero la sua trasformata di Fourier S(f) = 0 per ׀ f ׀ > BW (bandwidth)
il che significa che le componenti del segnale con frequenze maggiore della BW sono nulle
Fc = 1 / Tc > 2BW
cioè la frequenza di campionamento è maggiore ( o uguale) al doppio della banda allora:
Il segnale s(t) è rappresentato completamente dai suoi campioni
Il segnale s(t) può essere ricostruito nella sua forma originale con un filtro passa-basso avente frequenza di taglio Ft tale che BW < Ft.
In caso di un segnale con banda passante (ossia con frequenza inferiore diversa da zero) il teorema tiene conto di questo ed afferma:
sia BW = FH – FL, la larghezza di banda di un segnale con FH l’estremo superiore e FL l’estremo inferiore della banda, per evitare la sovrapposizione dello spettro campionato, la frequenza di campionamento deve soddisfare la seguente espressione matematica:
2(FL + BW) / N+1 < FC < 2FL / N con N < FL / BW (intero)
ciascun valore dell’intero N, incluso lo zero, fornisce un intervallo permesso di frequenze di campionamento.
Consideriamo il seguente esempio con FH = 2100kHz e FL = 1550kHz.
Si ha N < 2,8 ; N = 2,1,0.
Per cui gli intervalli permessi di frequenze di campionamento sono:
N = 2 : 1400kHz < Fc < 1550kHz
N = 1: 2100kHz < Fc < 3100kHz,
N = 0: 4200kHz < Fc.
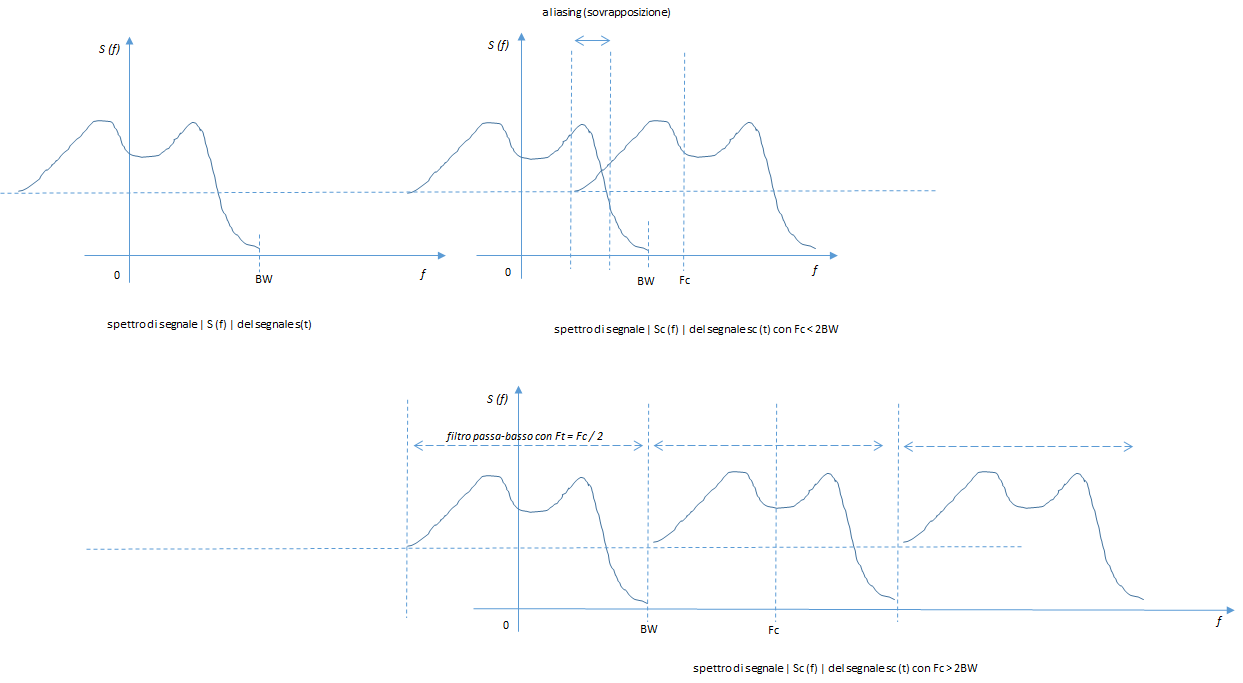
Dire che il passo di campionamento deve essere almeno il doppio la banda del segnale significa che gli spettri ripetuti ogni FC non si sovrappongono tra loro, evitando il fenomeno conosciuto come “aliasing”:
N.B.
Nella realtà non esistono segnali con banda strettamente limitata.
Per questo motivo si introduce, a monte del campionatore, un filtro passa basso (detto filtro anti-aliasing) che elimina le componenti di segnale in modo da rispettare il teorema sopra enunciato.